
 By RavensKrag
Date
By RavensKrag
Date 2014-08-17 05:32
Edited 2014-08-17 05:40
The problems you describe in #2 and #3 have to do with differences in coordinate systems. This is something that the current tutorial does not explain very well at all. I certainly struggled with it myself when I was getting started.
Please feel free to ask questions. This is the first time I've tried explaining the notion of coordinate systems.
(Hopefully I'll compile this info along with some other stuff into a proper Chipmunk tutorial when I have more free time)
This first part is an explanation of how coordinate systems are relevant to this problem.
The second post (right under this one) uses this information to answer your questions.
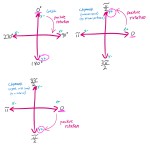
Take a look at this diagram.
[ATTACHED BELOW, can't figure out how to inline at proper size]
The illustration of Gosu's coordinate system is how the Gosu window is set up. That's rather definitive (though, like most things in programming, you could alter it if you really wanted).
However, you can interpret the data from Chipmunk in various ways. Chipmunk is just a physics library. It does not really specify how data is to be visualized. I prefer to think of the positive direction of the Y-Axis as being "up", but you could interpret that data as "down" if you wanted to. (In particular, the tutorial seems to use y+ DOWN, so I have illustrated both.)
In fact, specifying y+ DOWN may make combining Gosu and Chipmunk more straightforward. If you look at the diagram, you'll notice that the three differences between these coordinate systems are:
1) y+ DOWN (vs) y+ UP
2) positive rotation clockwise (vs) positive rotation COUNTER-clockwise
3) 0 is UP (vs) 0 is RIGHT
Points (1) and (2) are linked.
When you flip your interpretation of the Chipmunk Y-Axis, your interpretation of positive rotation direction with be altered as well. PI/2 is always attached to the Y+ axis, regardless of where that may lie. Same goes for any other axis and angle measure pair.
Even after interpreting both Chipmunk and Gosu as y+ DOWN, you will find that the 0 angle measures will not match up. They will always be out of sync by a quarter turn.
However, you can't just change your interpretation of which angles are associated with which axes. Doing so would mean the numbers Chipmunk gives you concerning rotations would cease to make sense. Chipmunk's internal math assumes a coordinate system with a certain angle and axis relationship (I'm not sure of the formal term for this).
I suggest implementing some sort of method to allow for easy conversion between Chipmunk's coordinate space and Gosu's coordinate space (and vice versa) so that it is always clear that a coordinate space conversion is happening, and not some other sort of angular math.
I will assume you understand the difference between angles and radians, and can convert between the two appropriately. The specifics of how you want to write the conversion methods are up to you. Do you want to create methods like radians_to_degrees(angle), or will you monkey-patch Numeric to provide Numeric#to_degrees and Numeric#to_radians. Do you want conflate conversion between radians and degrees with the coordinate space conversion? Or do you want to keep those two ideas separate? There are many choices to be made at this point, but I'm not certain there is a "best" answer. It seems like more of an issue of personal coding style.
With these things in mind, I will return to your questions:
I'm going to answer #3 first, because #2 is dependent on #3
#3:
In the coordinate system I tend to use, verticies should always be specified clockwise. If you would prefer to use a y+ DOWN coordinate system, (as is consistent with Gosu's coordinate system) then yes, the verticies should be specified counter-clockwise. In either case, the verticies should be specified in order of decreasing rotation. CW / CCW is relative to the coordinate system you use the interpret the data, but the direction of positive rotation is determined by Chipmunk. It makes assumptions about rotations, sometimes referred to as the "handedness" of a coordinate system (as in "right handed" or "left handed"), to return correct signage for things like the cross product.
I think when you say "bottom-left vertex" you are using the same coordinate system as the one I tend to use with Chipmunk. However, I believe the tutorial uses an y+ DOWN coordinate system. This means the first vertex is actually the TOP LEFT point. In general, the top-left of an image is the origin of that image (this applies to all image formats that I know of, not just Gosu::Image objects). Thus, the top-left is generally specified first, simply because it is the origin.
#2:
The coordinate systems are tripping you up again.
Here's a diagram which explains how the example lists verts for the shape of the ship:
[ATTACHED BELOW, can't figure out how to inline at proper size]
What we're going to do is rotate the shape so that it is correct in Chipmunk coordinate space, and then transform the data such that the sprite can be rendered correctly in Gosu coordinate space.
In the end, the ship ends up rendered on screen pointing up, because the sprite is being drawn with a rotation of 0 degrees in Gosu coordinate space (see first diagram for refresher).
However, UP in Chipmunk coordinate space (again, we're assuming y+ DOWN) is 3 PI / 2. We thus want @player.shape.body.a == 3 * Math::PI / 2. This means rotating the ship a quarter turn CCW from it's initial orientation of 0 radians. Knowing that we want the final result to point UP, and that we need to turn the body a quarter turn CCW, we must specify the verticies such that the ship points to the right in its default orientation. (Notice that RIGHT is a quarter turn CW from UP)
At this point, you may think:
"why not just rotate the body BEFORE the verticies are applied?"
That's unfortunately not how this works.
This is another case of coordinate space conversion.
The shape verticies are specified (and stored) in a coordinate space relative to the body. In order to evaluate collisions, all shapes are converted to global coordinate space. In fact, Chipmunk actually exposes world2local and local2world if you ever need to convert between those coordinate systems.
Thus, you can't simply rotate the body ahead of time, because that rotation is not applied until the shape verticies are converted from local space to world space. This conversion needs to done repeatedly inside of CP::Space to account for both the rotation and translation of objects.
But the heavy-lifting behind that is why you're using Chipmunk :D
In summary:
Switching between coordinate systems can be really confusing, and confusion causes bugs. Thus, I once again recommend that you write methods to perform coordinate space conversion, rather than writing it out each time. It's not just because you're a beginner. I still get tripped up by this stuff sometimes.
(Also, man. I had forgotten how bad that tutorial is. Ugh.)